Jan von Bassewitz
vbjan[at]ethz[dot]ch
Data Science MSc, Mechanical Eng BSc
Numerical Approximation of the Stationary Reaction Diffusion Equation on L-shape Domain
Keywords: computational science
This is a part of my final project of the course Computational Methods for Engineering Applications that I finished in my fifth semester. The goal of the project was to solve the stationary reaction diffusion equation on a L-shape domain, which is why a FEM-approach instead of a finite difference approach was chosen.
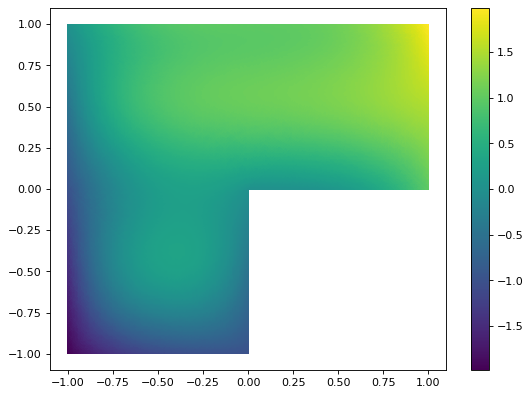
The differential equation reads:
\[-\nabla(\sigma \nabla u) + ru = f(x) \ \text{in} \ \Omega \subset \mathbb{R}^2 \\ u(x) = g(X) \ \text{on} \ \partial \Omega\]The code allows for different functions \(\sigma\), \(f\) and boundary conditions \(g\) to be implemented. The plot on the left results when choosing
\[\sigma(x,y) = 0.01 (x+2)^2, \\ f(x,y)=\sin(\pi y)^2, \\ r = 0.5, \\ g(x,y)=x^3+y.\]